imported>Soleverlee |
小 Riguz移动页面插入排序至Insertion Sort,不留重定向 |
||
| (未显示1个用户的6个中间版本) | |||
| 第1行: | 第1行: | ||
插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。 | 插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。 | ||
=算法描述= | =算法描述= | ||
[[Image:Insertion-sort-example-300px.gif|right|frame|使用插入排序为一列数字进行排序的过程]] | |||
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下: | 一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下: | ||
#从第一个元素开始,该元素可以认为已经被排序 | #从第一个元素开始,该元素可以认为已经被排序 | ||
| 第9行: | 第10行: | ||
#重复步骤2~5 | #重复步骤2~5 | ||
如果比较操作的代价比交换操作大的话,可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种,称为二分查找插入排序。 | 如果比较操作的代价比交换操作大的话,可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种,称为二分查找插入排序。 | ||
=示例代码= | =示例代码= | ||
==C== | ==C== | ||
| 第24行: | 第26行: | ||
</source> | </source> | ||
==C++= | ==C++== | ||
<source lang="cpp"> | |||
template<typename T> //整数或者浮点数都可以可使用,若要使用类(class)时必须设置大于(>)的比较功能 | |||
void insertion_sort(T arr[], int len) { | |||
int i, j; | |||
T temp; | |||
for (i = 1; i < len; i++) { | |||
temp = arr[i]; | |||
for (j = i - 1; j >= 0 && arr[j] > temp; j--) | |||
arr[j + 1] = arr[j]; | |||
arr[j + 1] = temp; | |||
} | |||
} | |||
template<typename T> | |||
void insertion_sort(T *first, T *last) { | |||
T *i, *j, temp; | |||
for (i = first + 1; i <= last; i++) { | |||
temp = *i; | |||
for (j = i - 1; j >= first && *j > temp; j--) | |||
*(j + 1) = *j; | |||
*(j + 1) = temp; | |||
} | |||
} | |||
</source> | |||
==C#== | ==C#== | ||
<source lang="csharp"> | |||
public static void InsertSort(double[] data) { | |||
int i, j; | |||
var count = data.Length; | |||
for (i = 1 ; i < count ; i++) { | |||
var t = data[i]; | |||
for(j = i - 1; j >= 0 && data[j] > t; j--) | |||
data[j + 1] = data[j]; | |||
data[j + 1] = t; | |||
} | |||
} | |||
</source> | |||
==Java== | ==Java== | ||
<source lang="java"> | |||
public class Insertion { | |||
public static void insertionSort(Comparable []data) { | |||
for(int index = 1; index < data.length; index++) { | |||
Comparable key = data[index]; | |||
int position = index; | |||
//shift larger values to the right | |||
while (position > 0 && data[position - 1].compareTo(key) > 0) { | |||
data[position] = data[position - 1]; | |||
position--; | |||
} | |||
data[position] = key; | |||
} | |||
} | |||
public static void main(String []args) { | |||
Comparable []c = {4, 9, 23, 1, 45, 27, 5, 2}; | |||
insertionSort(c); | |||
for(int i = 0; i < c.length; i++) | |||
System.out.println("插入排序:" + c[i]); | |||
} | |||
} | |||
</source> | |||
==Python== | ==Python== | ||
[Category:Algorithm] | <source lang="python"> | ||
def insertion_sort(n): | |||
if len(n) == 1: | |||
return n | |||
b = insertion_sort(n[1:]) | |||
m = len(b) | |||
for i in range(m): | |||
if n[0] <= b[i]: | |||
return b[:i]+[n[0]]+b[i:] | |||
return b + [n[0]] | |||
#另一个版本 | |||
def insertion_sort(lst): | |||
if len(lst) == 1: | |||
return | |||
for i in xrange(1, len(lst)): | |||
temp = lst[i] | |||
j = i - 1 | |||
while j >= 0 and temp > lst[j]: | |||
lst[j + 1] = lst[j] | |||
j -= 1 | |||
lst[j + 1] = temp | |||
</source> | |||
[[Category:Algorithm]] | |||
2024年1月18日 (四) 09:19的最新版本
插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
算法描述
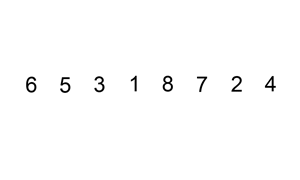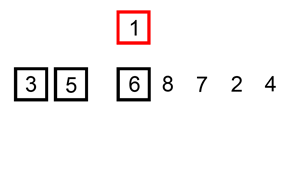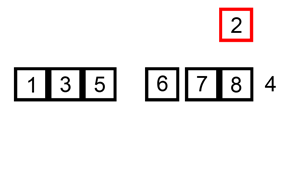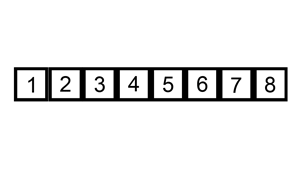
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
如果比较操作的代价比交换操作大的话,可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种,称为二分查找插入排序。
示例代码
C
void insertion_sort(int array[], int first, int last){
int i, j, temp;
for (i = first + 1; i <= last; i++){
temp = array[i]; //与已排序的数逐一比较,大于temp时,该数向后移
//当first=0,j循环到-1时,由于[[短路求值]],不会运算array[-1]
for(j = i - 1; j >= first && array[j] > temp; j--)
array[j + 1] = array[j];
array[j+1] = temp; //被排序数放到正确的位置
}
}
C++
template<typename T> //整数或者浮点数都可以可使用,若要使用类(class)时必须设置大于(>)的比较功能
void insertion_sort(T arr[], int len) {
int i, j;
T temp;
for (i = 1; i < len; i++) {
temp = arr[i];
for (j = i - 1; j >= 0 && arr[j] > temp; j--)
arr[j + 1] = arr[j];
arr[j + 1] = temp;
}
}
template<typename T>
void insertion_sort(T *first, T *last) {
T *i, *j, temp;
for (i = first + 1; i <= last; i++) {
temp = *i;
for (j = i - 1; j >= first && *j > temp; j--)
*(j + 1) = *j;
*(j + 1) = temp;
}
}
C#
public static void InsertSort(double[] data) {
int i, j;
var count = data.Length;
for (i = 1 ; i < count ; i++) {
var t = data[i];
for(j = i - 1; j >= 0 && data[j] > t; j--)
data[j + 1] = data[j];
data[j + 1] = t;
}
}
Java
public class Insertion {
public static void insertionSort(Comparable []data) {
for(int index = 1; index < data.length; index++) {
Comparable key = data[index];
int position = index;
//shift larger values to the right
while (position > 0 && data[position - 1].compareTo(key) > 0) {
data[position] = data[position - 1];
position--;
}
data[position] = key;
}
}
public static void main(String []args) {
Comparable []c = {4, 9, 23, 1, 45, 27, 5, 2};
insertionSort(c);
for(int i = 0; i < c.length; i++)
System.out.println("插入排序:" + c[i]);
}
}
Python
def insertion_sort(n):
if len(n) == 1:
return n
b = insertion_sort(n[1:])
m = len(b)
for i in range(m):
if n[0] <= b[i]:
return b[:i]+[n[0]]+b[i:]
return b + [n[0]]
#另一个版本
def insertion_sort(lst):
if len(lst) == 1:
return
for i in xrange(1, len(lst)):
temp = lst[i]
j = i - 1
while j >= 0 and temp > lst[j]:
lst[j + 1] = lst[j]
j -= 1
lst[j + 1] = temp