无编辑摘要 |
|||
| (未显示同一用户的13个中间版本) | |||
| 第11行: | 第11行: | ||
其中,consensus module用来保证log的复制是正确的,也就是paxos要解决的问题。 | 其中,consensus module用来保证log的复制是正确的,也就是paxos要解决的问题。 | ||
那么,对于这样一个系统有哪些要求呢? | |||
* 所有的服务器将以同样的顺序执行相同的命令 | |||
* 只要集群中大多数服务器可用,系统就是可用状态 | |||
=Paxos算法= | =Paxos算法= | ||
| 第33行: | 第39行: | ||
另外,paxos中是不考虑拜占庭问题的,有如下假设成立: | 另外,paxos中是不考虑拜占庭问题的,有如下假设成立: | ||
* Agents operate at arbitrary speed, may fail by stopping, and may restart. Since all agents may fail after a value is chosen and then restart, a solution is impossible unless some information can be <span class="article-label">re- membered</span> by an agent that has failed and restarted. | * Agents operate at arbitrary speed, may fail by stopping, and may restart. Since all agents may fail after a value is chosen and then restart, a solution is impossible unless some information can be <span class="article-label">re- membered</span> by an agent that has failed and restarted. | ||
* Messages can take arbitrarily long to be delivered, can be duplicated, and can be lost, but they are <span class="article-label">not corrupted</span>. | * Messages can take arbitrarily long to be delivered, can be duplicated, and can be lost, but they are <span class="article-label">not corrupted</span>. 也即是 <span class="article-label">fail-stop/crash</span> (non-Byzantine) and <span class="article-label">message delay/loss</span> | ||
==Choosing a Value== | |||
===Quorum=== | |||
Paxos made simple中,从最简单(但不正确)的方式开始,逐步加强约束,最终得到正确的算法。 | |||
首先最简单的情况下,只有一个acceptor,然后choose第一个收到的提案。这种办法显然不行,因为一旦这个acceptor出问题了整个系统就没法用了,所以需要有多个acceptor,当系统中有大多数acceptor接受了提案则认为值被choosen。 | |||
为了在集群中形成多数派,其数目必须为基数,设集群中server总数为$$2F + 1$$,则至少可以由$$F+1$$个server构成多数派。 | |||
===P1=== | |||
如果仅有一个proposer提出了一个提案,那么这个提案显然是需要被接受的。也就是说,acceptor必须要接受它收到的第一个提案,否则如果只有一个proposal的时候就无法选出任何提案了。因此可推导出约束P1: | |||
<q> | |||
P1. An acceptor must accept the first proposal that it receives. | |||
</q> | |||
但是这样是有问题的,因为如果不同的proposal提出多个提议,分别被不同的acceptors接受,则无法形成多数派: | |||
[[File:Paxos-p1-issue.png|600px]] | |||
即使只有两个提案,如上图,如果其中一个acceptor失败则也无法知晓到底哪个值被choose了。 | |||
因此说,只允许acceptor接受一个提议是不行的。acceptor必须要能够允许接受多个提议。对于不同的proposal,以编号的形式来表示,则每个提议可表示为$$p_{i}(v)$$,即第$$i$$个提议值为$$v$$。 | |||
===P2=== | |||
为了解决P1的问题,可以允许acceptor接受多个提议,但是保证这些提议的值是一样的。也即: | |||
<q> | |||
P2. If a proposal with value v is chosen, then every higher-numbered proposal that is chosen has value v. | |||
</q> | |||
[[Category: | [[Category:Algorithm]] | ||
2024年7月3日 (三) 06:18的最新版本
Paxos解决的是什么问题
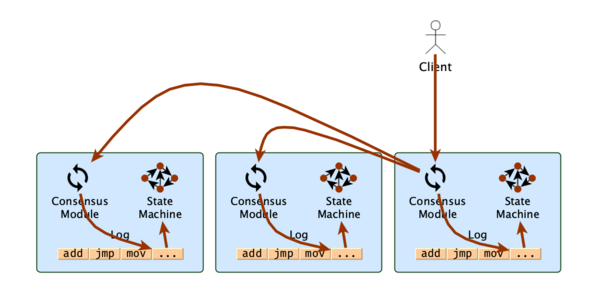
state machine replication
如上所示的系统中,如果客户端要执行某个命令,那么将遵循如下的步骤:
- 发送命令到其中某一个server
- server首先将命令记录到log中,然后将命令发送到其他的服务中;其他server同样将其记录到log中
- 当命令完整的记录到各个server之后,就可以传到state machine去执行了,并将结果返回给客户端
其中,consensus module用来保证log的复制是正确的,也就是paxos要解决的问题。
那么,对于这样一个系统有哪些要求呢?
- 所有的服务器将以同样的顺序执行相同的命令
- 只要集群中大多数服务器可用,系统就是可用状态
Paxos算法
The Paxos algorithm, when presented in plain English, is very simple.
共识问题
上述问题可以简化为,有多个服务可以propose value,而共识算法将保证有且仅有一个value会被选中(chosen)。这里面隐含的条件是:
- 如果没有任何value被propose,那么也不应该有任何值被选中
- 值一旦被选中,各个服务应该可以知晓(learn)选中的值
从而可以得出共识算法实现的安全性约束:
Safety requirements
- Validity (or non-triviality)
- Only a value that has been proposed may be chosen, A process never learns that a value has been chosen unless it actually has been.
- Agreement (or consistency, or safety)
- Only a single value is chosen, and
- Termination (or liveness)
- if a value has been chosen, then a process can eventually learn the value.
assumptions
另外,paxos中是不考虑拜占庭问题的,有如下假设成立:
- Agents operate at arbitrary speed, may fail by stopping, and may restart. Since all agents may fail after a value is chosen and then restart, a solution is impossible unless some information can be re- membered by an agent that has failed and restarted.
- Messages can take arbitrarily long to be delivered, can be duplicated, and can be lost, but they are not corrupted. 也即是 fail-stop/crash (non-Byzantine) and message delay/loss
Choosing a Value
Quorum
Paxos made simple中,从最简单(但不正确)的方式开始,逐步加强约束,最终得到正确的算法。
首先最简单的情况下,只有一个acceptor,然后choose第一个收到的提案。这种办法显然不行,因为一旦这个acceptor出问题了整个系统就没法用了,所以需要有多个acceptor,当系统中有大多数acceptor接受了提案则认为值被choosen。
为了在集群中形成多数派,其数目必须为基数,设集群中server总数为$$2F + 1$$,则至少可以由$$F+1$$个server构成多数派。
P1
如果仅有一个proposer提出了一个提案,那么这个提案显然是需要被接受的。也就是说,acceptor必须要接受它收到的第一个提案,否则如果只有一个proposal的时候就无法选出任何提案了。因此可推导出约束P1:
P1. An acceptor must accept the first proposal that it receives.
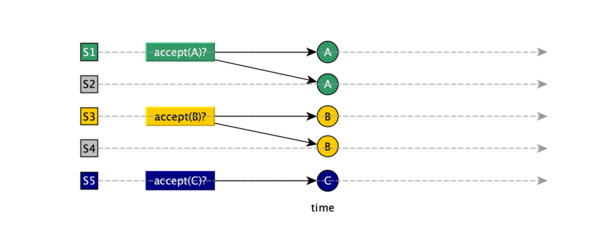
但是这样是有问题的,因为如果不同的proposal提出多个提议,分别被不同的acceptors接受,则无法形成多数派:
即使只有两个提案,如上图,如果其中一个acceptor失败则也无法知晓到底哪个值被choose了。
因此说,只允许acceptor接受一个提议是不行的。acceptor必须要能够允许接受多个提议。对于不同的proposal,以编号的形式来表示,则每个提议可表示为$$p_{i}(v)$$,即第$$i$$个提议值为$$v$$。
P2
为了解决P1的问题,可以允许acceptor接受多个提议,但是保证这些提议的值是一样的。也即:
P2. If a proposal with value v is chosen, then every higher-numbered proposal that is chosen has value v.