Recursion and iteration

这是读《计算机程序的构造和解释》的笔记。

递归和迭代

计算裴波拉切数列

裴波拉切数列是很简单的过程，其数学公式如下：

$$ Fib(n)=\left\{ \begin{array}{rcl} 0 & {n = 0}\\ 1 & {n = 1}\\ Fib(n-1) + Fib(n-2) & {n > 1}\\ \end{array} \right. $$

使用递归非常容易解决，就是直接将这个公式翻译成计算机语言即可：

(define (fib n)
    (cond 
        ((= n 0) 0)
        ((= n 1) 1)
        (else (+ (fib (- n 1))
                 (fib (- n 2)))
        )
    )
)

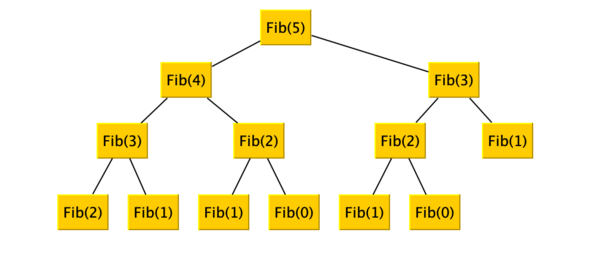
这个递归算法虽然实现很简单，但却有比较大的性能问题，出现了不必要的计算。例如计算Fib(5)，其计算过程如下：

其中Fib(2)就计算了三次。那么，如何使用迭代来计算呢？迭代的思想在于给定若干变量的初始值，不断根据规则进行计算来改变这些变量，最后进行N次之后得到最终的结果。

$$ \begin{cases} a = Fib(1) \\ b = Fib(0) \end{cases} \xrightarrow[\text{进行迭代}]{} \begin{cases} a = a + b \\ b = a \end{cases} \xrightarrow[\text{通过n次迭代变成}]{} \begin{cases} a = Fib(n+1)) \\ b = Fib(n) \end{cases} $$

这样实际上需要三个变量：

$$ \begin{cases} F_{n} \\ F_{n+1} \\ Count \end{cases} \xrightarrow[\text{初始值}]{} \begin{cases} F_{n} &= Fib(0)\\ F_{n+1} &= Fib(1) \\ Count &= n \end{cases} \xrightarrow[\text{第一次迭代}]{} \begin{cases} F_{n} &= Fib(1)\\ F_{n+1} &= Fib(0) + Fib(1) \\ Count &= n - 1 \end{cases}\\ \xrightarrow[\text{第n次迭代}]{} \begin{cases} F_{n} &= Fib(n)\\ F_{n+1} &= Fib(n-1) + Fib(n) \\ Count &= 0 \end{cases} $$

那么，翻译成代码就是：

(define (fib n)
     (fib_iter 1 0 n)
)

(define (fib_iter a b i)
    (if (= i 0)
        b
        (fib_iter (+ a b) a (- i 1))
    )
)