YATA algorithm:修订间差异
| (未显示同一用户的5个中间版本) | |||
| 第3行: | 第3行: | ||
== Rules == | == Rules == | ||
<q> | |||
We compose the following three rules in order to find a | |||
strict total order <math><_{c}</math> on conflicting operations. | |||
</q> | |||
strict total order(严格全序): A '''strict total order''' on a set <math>X</math> is a strict partial order on <math>X</math> in which any two distinct elements are comparable. That is, a strict total order is a binary relation <math><</math> on some Set <math>X</math>, which satisfies the following for all <math>a, b</math> and <math>c</math> in <math>X</math> | |||
<ref>https://en.wikipedia.org/wiki/Total_order</ref>: | |||
# Not <math>a < a</math> (irreflexive). | |||
# If <math>a < b</math> then not <math> b < a </math> (asymmetric). | |||
# If <math>a < b</math> and <math>b < c</math> then <math>a < c</math> (transitive). | |||
# If <math>a \neq b</math>, then <math>a < b</math> or <math>b < a</math> (connected). | |||
=== Rule1: No line crossing === | === Rule1: No line crossing === | ||
<q> | <q> | ||
| 第20行: | 第32行: | ||
=== Rule2: transitivity on <c === | === Rule2: transitivity on <c === | ||
transitivity: if 𝑎≤𝑏 and 𝑏≤𝑐, then 𝑎≤𝑐, for every 𝑎, 𝑏, and 𝑐 in 𝐴.<ref>https://leanprover.github.io/logic_and_proof/relations.html | transitivity: if 𝑎≤𝑏 and 𝑏≤𝑐, then 𝑎≤𝑐, for every 𝑎, 𝑏, and 𝑐 in 𝐴.<ref>https://leanprover.github.io/logic_and_proof/relations.html</ref> | ||
<q> | <q> | ||
| 第59行: | 第71行: | ||
<math> | <math> | ||
o_{1} \leq_{c} o_{2} \iff o_{1} <_{c} o_{2} \lor o_{1} \equiv o_{2} | o_{1} \leq_{c} o_{2} \iff o_{1} <_{c} o_{2} \quad \lor \quad o_{1} \equiv o_{2} | ||
</math> | </math> | ||
| 第68行: | 第80行: | ||
ordering function <math>c=<_{c}</math> is antisymmetric, transitive, and total. | ordering function <math>c=<_{c}</math> is antisymmetric, transitive, and total. | ||
</q> | </q> | ||
antisymmetric(反对称关系)<ref>https://zh.wikipedia.org/wiki/%E5%8F%8D%E5%AF%B9%E7%A7%B0%E5%85%B3%E7%B3%BB</ref>: | |||
<math>\displaystyle \forall a,b\in X,\ aRb\land bRa\;\Rightarrow \;a=b</math> | |||
<math> | <math> | ||
| 第74行: | 第89行: | ||
o_{1} \leq_{c} o_{2} \land o_{2} \leq_{c} o_{1} \quad &\implies \quad o_{1} \equiv o_{2} \quad (antisymmetry) \\ | o_{1} \leq_{c} o_{2} \land o_{2} \leq_{c} o_{1} \quad &\implies \quad o_{1} \equiv o_{2} \quad (antisymmetry) \\ | ||
o_{1} \leq_{c} o_{2} \land o_{2} \leq_{c} o_{3} \quad &\implies \quad o_{1} \leq_{c} o_{3} \quad (transitivity) \\ | o_{1} \leq_{c} o_{2} \land o_{2} \leq_{c} o_{3} \quad &\implies \quad o_{1} \leq_{c} o_{3} \quad (transitivity) \\ | ||
o_{1} \leq_{c} o_{2} \quad &\lor \quad o_{2} \leq_{c} o_{1} \quad (totality) | |||
\end{align} | \end{align} | ||
2024年8月15日 (四) 06:19的最新版本
Notes on YATA paper
This is notes on Near Real-Time Peer-to-Peer Shared Editing on Extensible Data Types[1].
Rules
We compose the following three rules in order to find a
strict total order [math]\displaystyle{ \lt _{c} }[/math] on conflicting operations.
strict total order(严格全序): A strict total order on a set [math]\displaystyle{ X }[/math] is a strict partial order on [math]\displaystyle{ X }[/math] in which any two distinct elements are comparable. That is, a strict total order is a binary relation [math]\displaystyle{ \lt }[/math] on some Set [math]\displaystyle{ X }[/math], which satisfies the following for all [math]\displaystyle{ a, b }[/math] and [math]\displaystyle{ c }[/math] in [math]\displaystyle{ X }[/math] [2]:
- Not [math]\displaystyle{ a \lt a }[/math] (irreflexive).
- If [math]\displaystyle{ a \lt b }[/math] then not [math]\displaystyle{ b \lt a }[/math] (asymmetric).
- If [math]\displaystyle{ a \lt b }[/math] and [math]\displaystyle{ b \lt c }[/math] then [math]\displaystyle{ a \lt c }[/math] (transitive).
- If [math]\displaystyle{ a \neq b }[/math], then [math]\displaystyle{ a \lt b }[/math] or [math]\displaystyle{ b \lt a }[/math] (connected).
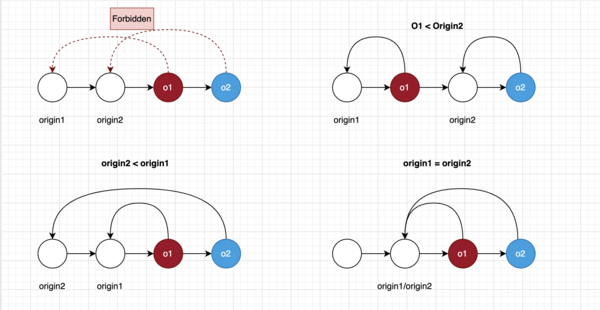
Rule1: No line crossing
Rule1: We forbid crossing of origin connections (red lines
in the graphical representation) between conflicting insertions. This rule is easily explained using the graphical representation of insertions in the linked list. As we stated
before, every insertion has an origin connection to an insertion to the left (to a predecessor). Only when two operations are concurrently inserted after the same insertion,
they will have the same origin.
[math]\displaystyle{ o1 \lt _{rule1} o2 \Leftrightarrow o1 \lt origin2 \lor origin2 \leq origin1 }[/math]
- Red line refers to the connection from the operation to it's origin
- The assumation is that o1 and o2 conflicts, which means that there's overlap between intentions of them.
Rule2: transitivity on <c
transitivity: if 𝑎≤𝑏 and 𝑏≤𝑐, then 𝑎≤𝑐, for every 𝑎, 𝑏, and 𝑐 in 𝐴.[3]
Specifies transitivity on [math]\displaystyle{ \lt _{c} }[/math]. Let [math]\displaystyle{ o_{1} \lt _{c} o_{2} }[/math]. Then
following rule ensures, that there is no [math]\displaystyle{ o }[/math] that is greater
than [math]\displaystyle{ o_{2} }[/math], but smaller than [math]\displaystyle{ o_{1} }[/math], with respect to [math]\displaystyle{ \lt _{c} }[/math]
[math]\displaystyle{ o_{1} \lt _{rule2} o_{2} \Leftrightarrow \exists o : o_{2} \lt _{c} o \to o_{1} \leq o \Leftrightarrow \nexists o : o_{2} \lt _{c} o \lt o_{1} }[/math]
Rule3: Smaller ID placed left
When two conflicting insertions have the same origin, the insertion with the smaller creator id is to the left.
We borrow this rule from the OT approach. But in OT this
rule is applied when the position parameters are equal.
[math]\displaystyle{ o_{1} \lt _{rule3} o_{2} \Leftrightarrow origin_{1} \equiv origin_{2} \to creator_{1} \lt creator_{2} }[/math]
We get retrieve the total order function [math]\displaystyle{ \lt _{c} }[/math] by enforcing all three rules:
[math]\displaystyle{ \begin{align} o_{1} \lt _{c} o_{2} &\iff (o_{1} \lt _{rule1} o_{2}) \land (o_{1} \lt _{rule2} o_{2}) \land (o_{1} \lt _{rule3} o_{2}) \\ &\Leftrightarrow \quad o1 \lt origin2 \lor origin2 \leq origin1 \\ &\land \quad \nexists o : o_{2} \lt _{c} o \lt o_{1} \\ &\land \quad origin_{1} \equiv origin_{2} \to creator_{1} \lt creator_{2} \end{align} }[/math]
and:
[math]\displaystyle{ o_{1} \leq_{c} o_{2} \iff o_{1} \lt _{c} o_{2} \quad \lor \quad o_{1} \equiv o_{2} }[/math]
Correctness
Therefore, we have to
show that for all conflicting insertions o1, o2, and o3 the
ordering function [math]\displaystyle{ c=\lt _{c} }[/math] is antisymmetric, transitive, and total.
antisymmetric(反对称关系)[4]: [math]\displaystyle{ \displaystyle \forall a,b\in X,\ aRb\land bRa\;\Rightarrow \;a=b }[/math]
[math]\displaystyle{ \begin{align} o_{1} \leq_{c} o_{2} \land o_{2} \leq_{c} o_{1} \quad &\implies \quad o_{1} \equiv o_{2} \quad (antisymmetry) \\ o_{1} \leq_{c} o_{2} \land o_{2} \leq_{c} o_{3} \quad &\implies \quad o_{1} \leq_{c} o_{3} \quad (transitivity) \\ o_{1} \leq_{c} o_{2} \quad &\lor \quad o_{2} \leq_{c} o_{1} \quad (totality) \end{align} }[/math]
- ↑ https://www.researchgate.net/publication/310212186_Near_Real-Time_Peer-to-Peer_Shared_Editing_on_Extensible_Data_Types
- ↑ https://en.wikipedia.org/wiki/Total_order
- ↑ https://leanprover.github.io/logic_and_proof/relations.html
- ↑ https://zh.wikipedia.org/wiki/%E5%8F%8D%E5%AF%B9%E7%A7%B0%E5%85%B3%E7%B3%BB