Shell Sort:修订间差异
小 Riguz移动页面希尔排序至Shell Sort,不留重定向 |
无编辑摘要 |
||
| 第14行: | 第14行: | ||
=示例代码= | =示例代码= | ||
==C== | ==C== | ||
< | |||
<syntaxhighlight lang="c++"> | |||
void shell_sort(int arr[], int len) { | void shell_sort(int arr[], int len) { | ||
int gap, i, j; | int gap, i, j; | ||
| 第26行: | 第27行: | ||
} | } | ||
} | } | ||
</ | </syntaxhighlight> | ||
==C++== | ==C++== | ||
< | |||
<syntaxhighlight lang="cpp"> | |||
template<typename T> //整数或者浮点数都可以可使用,若要使用类(class)时必须设置大于(>)的比较功能 | template<typename T> //整数或者浮点数都可以可使用,若要使用类(class)时必须设置大于(>)的比较功能 | ||
void shell_sort(T arr[], int len) { | void shell_sort(T arr[], int len) { | ||
| 第41行: | 第44行: | ||
} | } | ||
} | } | ||
</ | </syntaxhighlight> | ||
==Java== | ==Java== | ||
< | |||
<syntaxhighlight lang="java"> | |||
static <E extends Comparable<? super E>> void shellSort(List<E> a) { | static <E extends Comparable<? super E>> void shellSort(List<E> a) { | ||
int h = 1; | int h = 1; | ||
| 第60行: | 第65行: | ||
} | } | ||
} | } | ||
</ | </syntaxhighlight> | ||
[[Category:Algorithm]] | [[Category:Algorithm]] | ||
2024年1月18日 (四) 09:05的最新版本
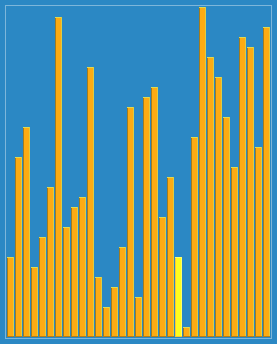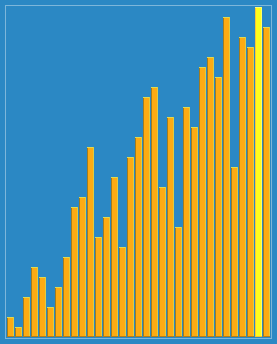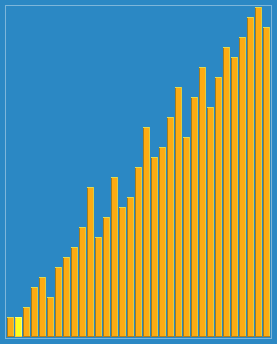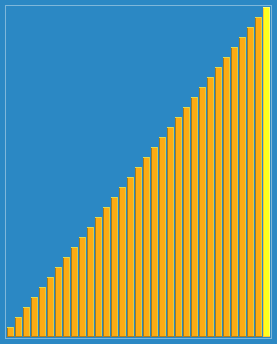
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
算法描述
- 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列个数k,对序列进行k 趟排序;
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
示例代码
C
void shell_sort(int arr[], int len) {
int gap, i, j;
int temp;
for (gap = len >> 1; gap > 0; gap >>= 1)
for (i = gap; i < len; i++) {
temp = arr[i];
for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
arr[j + gap] = arr[j];
arr[j + gap] = temp;
}
}
C++
template<typename T> //整数或者浮点数都可以可使用,若要使用类(class)时必须设置大于(>)的比较功能
void shell_sort(T arr[], int len) {
int gap, i, j;
T temp;
for (gap = len >> 1; gap > 0; gap >>= 1)
for (i = gap; i < len; i++) {
temp = arr[i];
for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
arr[j + gap] = arr[j];
arr[j + gap] = temp;
}
}
Java
static <E extends Comparable<? super E>> void shellSort(List<E> a) {
int h = 1;
while (h < a.size()/3) {
h = h*3 + 1; // <O(n^(3/2)) by Knuth,1973>: 1, 4, 13, 40, 121, ...
}
for (; h >= 1; h /= 3) {
for (k = 0; k < h; k++) {
for (int i = h + k; i < a.size(); i+=h) {
for (int j = i; j >= h && a.get(j).compareTo(a.get(j-h)) < 0; j-=h) {
Collections.swap(a, j, j-h);
}
}
}
}
}
