imported>Soleverlee 以“right|frame|使用快速排序法对一列数字进行排序的过程 快速排序是由东尼·霍尔所发展的一种排序...”为内容创建页面 |
imported>Soleverlee |
||
| 第11行: | 第11行: | ||
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会退出,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。 | 递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会退出,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。 | ||
=示例代码= | =示例代码= | ||
==C== | ==C++(迭代版本)== | ||
<source lang=" | <source lang="cpp"> | ||
//参考:http://www.dutor.net/index.php/2011/04/recursive-iterative-quick-sort/ | |||
struct Range{ | |||
explicit Range(int s=0,int e=0):start(s),end(e){} | |||
int start,end; | |||
}; | |||
void quicksort(int n,int arr[]){ | |||
if(n<=0) return; | |||
stack<Range> st; | |||
st.push(Range(0,n-1)); | |||
while(!st.empty()){ | |||
Range range = st.top(); | |||
st.pop(); | |||
int pivot = arr[range.end]; | |||
int pos = range.start-1; | |||
for(int i=range.start;i<range.end;++i){ | |||
if(arr[i]<pivot){ | |||
std::swap(arr[i],arr[++pos]); | |||
} | |||
} | |||
std::swap(arr[++pos],arr[range.end]); | |||
if(pos-1>range.start){ | |||
st.push(Range(range.start,pos-1)); | |||
} | |||
if(pos+1<range.end){ | |||
st.push(Range(pos+1,range.end)); | |||
} | |||
} | |||
} | |||
</source> | </source> | ||
==C== | ==C== | ||
<source lang="c"> | <source lang="c"> | ||
2015年3月27日 (五) 09:03的版本
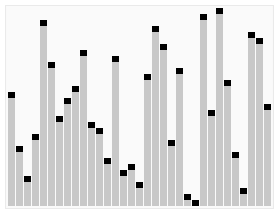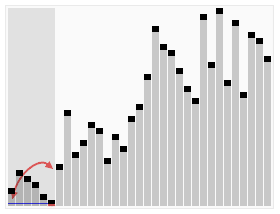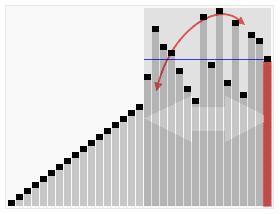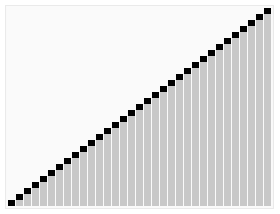
快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下,排序n个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较,但这种状况并不常见。事实上,快速排序通常明显比其他Ο(n log n)算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。
算法描述
快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。
步骤为:
- 从数列中挑出一个元素,称为"基准"(pivot),
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个#分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会退出,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
示例代码
C++(迭代版本)
//参考:http://www.dutor.net/index.php/2011/04/recursive-iterative-quick-sort/
struct Range{
explicit Range(int s=0,int e=0):start(s),end(e){}
int start,end;
};
void quicksort(int n,int arr[]){
if(n<=0) return;
stack<Range> st;
st.push(Range(0,n-1));
while(!st.empty()){
Range range = st.top();
st.pop();
int pivot = arr[range.end];
int pos = range.start-1;
for(int i=range.start;i<range.end;++i){
if(arr[i]<pivot){
std::swap(arr[i],arr[++pos]);
}
}
std::swap(arr[++pos],arr[range.end]);
if(pos-1>range.start){
st.push(Range(range.start,pos-1));
}
if(pos+1<range.end){
st.push(Range(pos+1,range.end));
}
}
}