imported>Soleverlee 以“right|frame|首先,将元素进行重排,以符合堆的条件。图中排序过程之前简单的绘出了堆树的结构。...”为内容创建页面 |
imported>Soleverlee |
||
| 第12行: | 第12行: | ||
<source lang="c"> | <source lang="c"> | ||
#define MAX_HEAP_LEN 100 | #define MAX_HEAP_LEN 100 | ||
static int heap[MAX_HEAP_LEN]; | |||
static int heap_size = 0; // the number of elements in heaps | |||
static void swap(int* a, int* b) | |||
{ | |||
int temp = *b; | |||
*b = *a; | |||
*a = temp; | |||
} | |||
static void shift_up(int i) | |||
{ | |||
int done = 0; | |||
if( i == 0) return; //node is the root already | |||
while((i!=0)&&(!done)) | |||
{ | |||
if(heap[i] > heap[(i-1)/2]) | |||
{//if the current is larger than the parent, then swap | |||
swap(&heap[i],&heap[(i-1)/2]); | |||
} | |||
else | |||
{// the job is already done. | |||
done =1; | |||
} | |||
i = (i-1)/2; | |||
} | |||
} | |||
static void shift_down(int i) | |||
{ | |||
int done = 0; | |||
if (2*i + 1> heap_size) return; // node i is a leaf | |||
while((2*i+1 < heap_size)&&(!done)) | |||
{ | |||
i =2*i+1; // jump to left child | |||
if ((i+1< heap_size) && (heap[i+1] > heap[i])) | |||
{// find the bigger one of the two children | |||
i++; | |||
} | |||
if (heap[(i-1)/2] < heap[i]) | |||
{ | |||
swap(&heap[(i-1)/2], &heap[i]); | |||
} | |||
else | |||
{ | |||
done = 1; | |||
} | |||
} | |||
} | |||
static void delete(int i) | |||
{ | |||
int last = heap[heap_size - 1]; // get the last one; | |||
heap_size--; // shrink the heap | |||
if (i == heap_size) return; | |||
heap[i] = last; // use the last item to overwrite the current | |||
shift_down(i); | |||
} | |||
int delete_max() | |||
{ | |||
int ret = heap[0]; | |||
delete(0); | |||
return ret; | |||
} | |||
void insert(int new_data) | |||
{ | |||
if(heap_size >= MAX_HEAP_LEN) return; | |||
heap_size++; | |||
heap[heap_size - 1] = new_data; | |||
shift_up(heap_size - 1); | |||
} | |||
</source> | </source> | ||
==C== | ==C== | ||
<source lang="c"> | <source lang="c"> | ||
2015年3月27日 (五) 09:55的版本
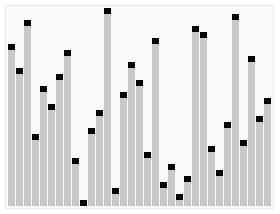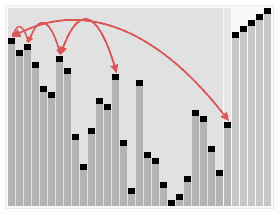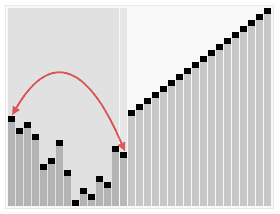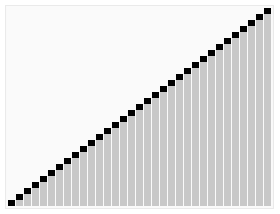
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
堆排序的平均时间复杂度为Ο(nlogn) 。
算法描述
- 创建一个堆H[0..n-1]
- 把堆首(最大值)和堆尾互换
- 把堆的尺寸缩小1,并调用shift_down(0),目的是把新的数组顶端数据调整到相应位置
- 重复步骤2,直到堆的尺寸为1
示例代码
C
#define MAX_HEAP_LEN 100
static int heap[MAX_HEAP_LEN];
static int heap_size = 0; // the number of elements in heaps
static void swap(int* a, int* b)
{
int temp = *b;
*b = *a;
*a = temp;
}
static void shift_up(int i)
{
int done = 0;
if( i == 0) return; //node is the root already
while((i!=0)&&(!done))
{
if(heap[i] > heap[(i-1)/2])
{//if the current is larger than the parent, then swap
swap(&heap[i],&heap[(i-1)/2]);
}
else
{// the job is already done.
done =1;
}
i = (i-1)/2;
}
}
static void shift_down(int i)
{
int done = 0;
if (2*i + 1> heap_size) return; // node i is a leaf
while((2*i+1 < heap_size)&&(!done))
{
i =2*i+1; // jump to left child
if ((i+1< heap_size) && (heap[i+1] > heap[i]))
{// find the bigger one of the two children
i++;
}
if (heap[(i-1)/2] < heap[i])
{
swap(&heap[(i-1)/2], &heap[i]);
}
else
{
done = 1;
}
}
}
static void delete(int i)
{
int last = heap[heap_size - 1]; // get the last one;
heap_size--; // shrink the heap
if (i == heap_size) return;
heap[i] = last; // use the last item to overwrite the current
shift_down(i);
}
int delete_max()
{
int ret = heap[0];
delete(0);
return ret;
}
void insert(int new_data)
{
if(heap_size >= MAX_HEAP_LEN) return;
heap_size++;
heap[heap_size - 1] = new_data;
shift_up(heap_size - 1);
}