YATA algorithm

Notes on YATA paper

This is notes on Near Real-Time Peer-to-Peer Shared Editing on Extensible Data Types.

Rules

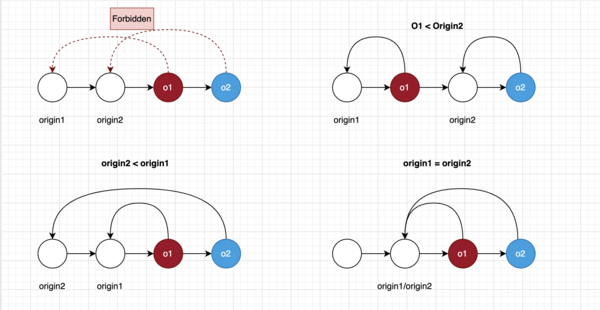
Rule1: No line crossing

Rule1: We forbid crossing of origin connections (red lines in the graphical representation) between conflicting insertions. This rule is easily explained using the graphical representation of insertions in the linked list. As we stated before, every insertion has an origin connection to an insertion to the left (to a predecessor). Only when two operations are concurrently inserted after the same insertion, they will have the same origin.

[math]\displaystyle{ o1 \lt _{rule1} o2 ⇔ o1 \lt origin2 ∨ origin2 ≤ origin1 }[/math]

• Red line refers to the connection from the operation to it's origin
• The assumation is that o1 and o2 conflicts, which means that there's overlap between intentions of them.

Rule2: transitivity on <c

transitivity: if 𝑎≤𝑏 and 𝑏≤𝑐, then 𝑎≤𝑐, for every 𝑎, 𝑏, and 𝑐 in 𝐴.

Specifies transitivity on [math]\displaystyle{ \lt _{c} }[/math]. Let [math]\displaystyle{ o_{1} \lt _{c} o_{2} }[/math]. Then following rule ensures, that there is no [math]\displaystyle{ o }[/math] that is greater than [math]\displaystyle{ o_{2} }[/math], but smaller than [math]\displaystyle{ o_{1} }[/math], with respect to [math]\displaystyle{ \lt _{c} }[/math]

[math]\displaystyle{ o_{1} \lt _{rule2} o_{2} \iff \exists o : o_{2} \lt _{c} o \to o_{1} \leq o \iff \nexists o : o_{2} \lt _{c} o \lt o_{1} }[/math]

Rule3: Smaller ID placed left

When two conflicting insertions have the same origin, the insertion with the smaller creator id is to the left. We borrow this rule from the OT approach. But in OT this rule is applied when the position parameters are equal.

[math]\displaystyle{ o_{1} \lt _{rule3} o_{2} ⇔ origin_{1} \equiv origin_{2} \to creator_{1} \lt creator_{2} }[/math]