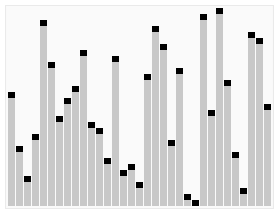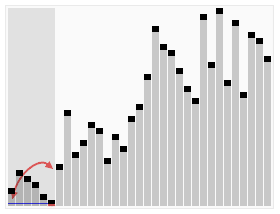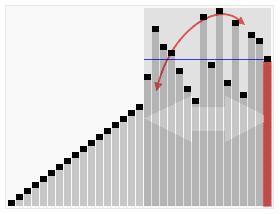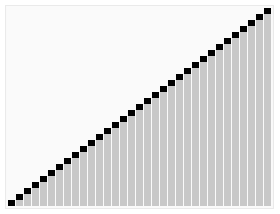
快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序n个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他Ο(n log n)算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。

算法描述

快速排序使用分治法（Divide and conquer）策略来把一个序列（list）分为两个子序列（sub-lists）。

步骤为：

从数列中挑出一个元素，称为"基准"（pivot），
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个#分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

示例代码

C++(迭代版本）

//参考：http://www.dutor.net/index.php/2011/04/recursive-iterative-quick-sort/
struct Range{
	explicit Range(int s=0,int e=0):start(s),end(e){}
	int start,end;
};
void quicksort(int n,int arr[]){
	if(n<=0) return;
	stack<Range> st;
	st.push(Range(0,n-1));
	while(!st.empty()){
		Range range = st.top();
		st.pop();
		int pivot = arr[range.end];
		int pos = range.start-1;
		for(int i=range.start;i<range.end;++i){
			if(arr[i]<pivot){
				std::swap(arr[i],arr[++pos]);
			}
		}
		std::swap(arr[++pos],arr[range.end]);
		if(pos-1>range.start){
			st.push(Range(range.start,pos-1));
		}
		if(pos+1<range.end){
			st.push(Range(pos+1,range.end));
		}
	}
}

C

#include <stdio.h>
#include <stddef.h>
 
void swap(int * a, int * b) {
  int tmp = * a;
  * a = * b;
  * b = tmp;
}
 
size_t partition(int * ary, size_t len, size_t pivot_i) {
  size_t i = 0;
  size_t small_len = pivot_i;
  int pivot = ary[pivot_i];
  swap(&ary[pivot_i], &ary[pivot_i + (len - 1)]);
  for (; i < len; i++) {
    if (ary[pivot_i + i] < pivot) {
      swap(&ary[pivot_i + i], &ary[small_len]);
      small_len++;
    }
  }
  swap(&ary[pivot_i + (len - 1)], &ary[small_len]);
  return small_len;
}
 
void quick_sort(int * ary, size_t len) {
  if (len == 0 || len == 1) return;
  size_t small_len = partition(ary, len, 0);
  quick_sort(ary, small_len);
  quick_sort(&ary[small_len + 1], len - small_len - 1);
}
 
int main(void) {
  int ary[] = {2,4,2,5,3,5,3,1,7,6};
  size_t len = sizeof(ary) / sizeof(ary[0]);
  quick_sort(ary, len);
  return 0;
}

C89标准在stdlib.h中定义了抽象数据类型的快速排序函数qsort(3)。

#include <stdio.h>
#include <stdlib.h>
 
static int cmp(const void *a, const void *b)
{
    return *(int *)a - *(int *)b;
}
int main()
{
    int arr[10]={5, 3, 7, 4, 1, 9, 8, 6, 2,10};
 
    qsort(arr, 10, sizeof(int), cmp);
 
    return 0;
}

#include <functional>
#include <algorithm>
#include <iterator>
 
template< typename BidirectionalIterator, typename Compare >
void quick_sort( BidirectionalIterator first, BidirectionalIterator last, Compare cmp ) {
  if( first != last ) {
    BidirectionalIterator left = first;
    BidirectionalIterator right = last;
    BidirectionalIterator pivot = left++;
 
    while( left != right ) {
      if( cmp( *left, *pivot ) ) {
         ++left;
      } else {
         while( (left != right) && cmp( *pivot, *right ) )
           right--;
         std::iter_swap( left, right );
      }
    }
 
    if (cmp( *pivot, *left ))
         --left;
    std::iter_swap( first, left );
 
    quick_sort( first, left, cmp );
    quick_sort( right, last, cmp );
  }
}
 
template< typename BidirectionalIterator >
inline void quick_sort( BidirectionalIterator first, BidirectionalIterator last ) {
  quick_sort( first, last,
    std::less_equal< typename std::iterator_traits< BidirectionalIterator >::value_type >()
  );
}

未使用STL的快速排序版本:

#include <utility>
using std::swap;
 
int partition(int* array, int left, int right)
{
	int index = left;
	int pivot = array[index];	
	swap(array[index], array[right]);
	for (int i=left; i<right; i++)
	{
		if (array[i] > pivot)    // 降序
			swap(array[index++], array[i]);
	}
	swap(array[right], array[index]);
	return index;
}
 
void qsort(int* array, int left, int right)
{
	if (left >= right) 
		return;
	int index = partition(array, left, right);
	qsort(array, left, index - 1);
	qsort(array, index + 1, right);
}

C#

public static void Sort(int[] numbers)
{
	Sort(numbers, 0, numbers.Length - 1);
}

private static void Sort(int[] numbers, int left, int right)
{
	if (left < right)
	{
		int middle = numbers[(left + right) / 2];
		int i = left - 1;
		int j = right + 1;
		while (true)
		{
			while (numbers[++i] < middle) ;

			while (numbers[--j] > middle) ;

			if (i >= j)
				break;

			Swap(numbers, i, j);
		}

		Sort(numbers, left, i - 1);
		Sort(numbers, j + 1, right);
	}
}

private static void Swap(int[] numbers, int i, int j)
{
	int number = numbers[i];
	numbers[i] = numbers[j];
	numbers[j] = number;
}

Python

def qsort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        return qsort([x for x in arr[1:] if x < pivot]) + \
               [pivot] + \
               qsort([x for x in arr[1:] if x >= pivot])

Java

class QuickSort{
    public static void main(String[] args) {
        int arr[] = {9,4,8,3,1,2,5};
        System.out.println("Initial Array");
        System.out.println(Arrays.toString(arr));
        quickSort(arr, 0, arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
    private static void quickSort(int[] arr, int low, int high) {
        if(low < high){
            int pos = partition(arr, low, high);
            quickSort(arr, low, pos-1);
            quickSort(arr, pos+1, high);
        }
    }

    private static int partition(int[] arr, int low, int high) {
        int pivot = arr[high];           //以最右边的元素为轴
        int small = low - 1;             //记录比轴小的左侧元素区间[low - small]
        for(int k = low; k < high; k++){ //遍历low -> hight区间
            if(arr[k] <= pivot){         //如果发现元素小于等于轴，则将元素移动到左侧
                small++;                 //同时更新左侧元素区间
                swap(arr, k, small);
            }
        }
        int nextPivot = small + 1;
        swap(arr, high, nextPivot);      //将轴移动到左侧区间[low- small] pivot ->high 
        return nextPivot;                //返回轴的新位置
    }

    private static void swap(int[] arr, int k, int small) {
        int temp;
        temp = arr[k];
        arr[k] = arr[small];
        arr[small] = temp;
    }    
}