Notes on YATA paper
This is notes on Near Real-Time Peer-to-Peer Shared Editing on Extensible Data Types[1].
Rules
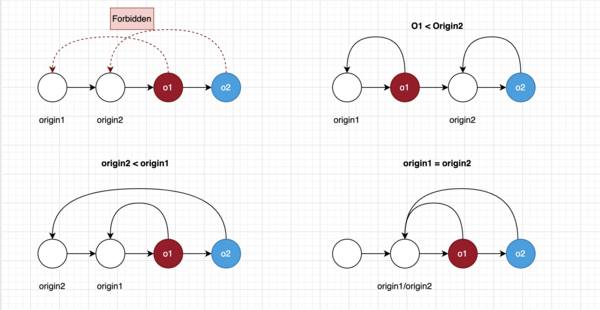
Rule1: No line crossing
Rule1: We forbid crossing of origin connections (red lines
in the graphical representation) between conflicting insertions. This rule is easily explained using the graphical representation of insertions in the linked list. As we stated
before, every insertion has an origin connection to an insertion to the left (to a predecessor). Only when two operations are concurrently inserted after the same insertion,
they will have the same origin.
[math]\displaystyle{ o1 \lt _{rule1} o2 \Leftrightarrow o1 \lt origin2 \lor origin2 \leq origin1 }[/math]
- Red line refers to the connection from the operation to it's origin
- The assumation is that o1 and o2 conflicts, which means that there's overlap between intentions of them.
Rule2: transitivity on <c
transitivity: if 𝑎≤𝑏 and 𝑏≤𝑐, then 𝑎≤𝑐, for every 𝑎, 𝑏, and 𝑐 in 𝐴.[2]
Specifies transitivity on [math]\displaystyle{ \lt _{c} }[/math]. Let [math]\displaystyle{ o_{1} \lt _{c} o_{2} }[/math]. Then
following rule ensures, that there is no [math]\displaystyle{ o }[/math] that is greater
than [math]\displaystyle{ o_{2} }[/math], but smaller than [math]\displaystyle{ o_{1} }[/math], with respect to [math]\displaystyle{ \lt _{c} }[/math]
[math]\displaystyle{ o_{1} \lt _{rule2} o_{2} \Leftrightarrow \exists o : o_{2} \lt _{c} o \to o_{1} \leq o \iff \nexists o : o_{2} \lt _{c} o \lt o_{1} }[/math]
Rule3: Smaller ID placed left
When two conflicting insertions have the same origin, the insertion with the smaller creator id is to the left.
We borrow this rule from the OT approach. But in OT this
rule is applied when the position parameters are equal.
[math]\displaystyle{ o_{1} \lt _{rule3} o_{2} \iff origin_{1} \equiv origin_{2} \to creator_{1} \lt creator_{2} }[/math]
We get retrieve the total order function [math]\displaystyle{ \lt _{c} }[/math] by enforcing all three rules:
[math]\displaystyle{ o_{1} \lt _{c} \iff (o_{1} \lt _{rule1} o_{2}) \land (o_{1} \lt _{rule2} o_{2}) \land (o_{1} \lt _{rule3} o_{2}) \\ \Leftrightarrow }[/math]